শূন্য, বীজগণিত আৰু তিনিটা যুগান্তকাৰী ঘটনা (পংকজজ্যোতি মহন্ত)

“Mathematics as an expression of the human mind reflects the active will, the contemplative reason, and the desire for aesthetic perfection. Its basic elements are logic and intuition, analysis and construction, generality and individuality.” – Richard Courant.

সামাজিক কাৰ্যকলাপ, মানসিক আচৰণ বা প্ৰাকৃতিক ঘটনা আদিৰ ক্ষেত্ৰত বিভিন্ন অন্ধবিশ্বাস থকাৰ দৰে বিজ্ঞান তথা প্ৰযুক্তিৰ ক্ষেত্ৰবোৰতো বহুতো অন্ধবিশ্বাস আছে। এনে অন্ধবিশ্বাসবোৰৰ পৰা মুক্ত মানুহৰ সংখ্যা যিমানে বেছি পৰিমাণৰ ফালে ধাৱিত হয়, সিমানে সমাজৰ মঙ্গল হ’ব বুলি আশা কৰিব পাৰি। গণিতত, এটা স্তৰত কিছুমান ফৰ্মুলা বা অৰ্হি খটুৱাই দিয়াৰ লগে লগেই প্ৰয়োজনীয় আনটো স্তৰ নিজে নিজে পাই যোৱা বুলি ভবাতো; ঠিক হাইস্কুলৰ ‘সৰল কৰা অংক’বোৰত পূৰ্বতে জনা কিছুমান ফৰ্মুলা আৰু ‘কটা–কটি’ আদিৰ কৌশল খটুৱাই দিলেই পাব লগা উত্তৰটো পাই যোৱাটোকেই গণিত বুলি ভবাটোও তেনে এটা অন্ধবিশ্বাস। ‘অংকটো কৰি গ’ল…’, এটা উত্তৰ ওলাল, লৰালৰিকৈ শেষৰ পিনৰ পৃষ্ঠাবোৰলৈ গৈ পতাপট ‘পাত লুটিয়াই’ উত্তৰটো চোৱা হ’ল, উত্তৰ মিলি গৈছে; বছ্, সি এটা চোকা ল’ৰা! এই দৃষ্টিভংগীৰেই , গণনাকেই (calculation) গণিত বুলি ভাবি থকা হয়। কিন্তু প্ৰকৃততে গণিত হ’ল, এই গণনা, ‘কটা–কটি’ বা ‘হাতে যোৱা’ আদি কিয় কৰিব পাৰি সেইটোহে বিচাৰি উলিওৱাটো। ইয়াৰ বাবে আমি ব্যৱহাৰ কৰি থকা সংখ্যাবোৰেই সৰ্বস্ব নহয়, এই সংখ্যাসমূহ কেৱল এটা সামান্য উপাদান বা সঁজুলিহে। এই কথাসমূহৰ সবিশেষ ভৱিষ্যতৰ আন এক প্ৰবন্ধৰ বাবে ৰাখি, এই সম্পৰ্কে সম্যক এটা ধাৰণা ল’ব পৰাকৈ শূন্যৰ লগত জড়িত তিনিটা যুগান্তকাৰী ঘটনাৰ কথা ক’ব বিচাৰিছোঁ। হাইস্কুলীয়া ছাত্ৰ–ছাত্ৰী বা হাইস্কুলৰ দেওনা পাৰ হোৱাৰ পাছত গণিত বিষয়টো নোলোৱা পাঠকেও বুজি পাব পৰাকৈ এই তিনিটা ঘটনা বাচি লোৱা হৈছে।

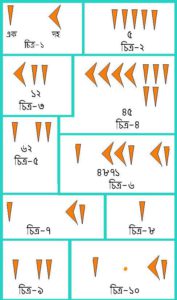
খ্ৰী.পূ. ১৬০০ ৰ পূৰ্বে বেবিলনীয়সকলে হিচাপ কৰিবলৈ কেৱল দুটা চিহ্ন ব্যৱহাৰ কৰিছিল। এটা ‘এক’ৰ বাবে আৰু আনটো ‘দহ’ৰ বাবে (চিত্ৰ–১)। চিত্ৰ–২, ৩ আৰু ৪ত তেওঁলোকে পাঁচ, বাৰ আৰু পঞ্চল্লিছক কেনেকৈ প্ৰকাশ কৰিছিল দেখুওৱা হৈছে। এনেদৰেই তেওঁলোকে ১ ৰ পৰা ৫৯ লৈকে সংখ্যাবোৰ প্ৰকাশ কৰিছিল। আৰু আমি বৰ্তমান দহৰ এটা এটা থুপ হিচাপে সংখ্যাবোৰ যেনেকৈ প্ৰকাশ কৰোঁ, তেওঁলোকে ষাঠিৰ থুপ হিচাপে আন সংখ্যাবোৰ প্ৰকাশ কৰিছিল। ২৩ ক আমি প্ৰকাশ কৰোঁ এইধৰণেৰে– ২X১০+৩ বা ৬২ ক ৬X১০+২ এইধৰণে বুজাও। তেনেকৈ তেওঁলোকে ষাঠিক ধৰি ষাঠিতকৈ ডাঙৰ সংখ্যাবোৰ প্ৰকাশ কৰিছিল, আৰু ষাঠিৰ স্থানটো বুজাবলৈ মাজত এটা খালি ঠাই ৰাখিছিল। আমি সাধাৰণ কামত বৰ্তমান সময়ত ১০ক ভেঁটি হিচাপে লওঁ, আৰু তেওঁলোকে ৬০ ক ভেঁটি হিচাপে লৈছিল । তেওঁলোকে ৬২ ক কেনেকৈ প্ৰকাশ কৰিছিল চিত্ৰ–৫ ত দেখুওৱা হৈছে। অৰ্থাৎ, আজিৰ ভাষাত ১X৬০+২ । গতিকে, ৪৮৭১ সংখ্যাটো প্ৰকাশ কৰিছিল চিত্ৰ–৬ ত দেখুওৱাৰ দৰে; কাৰণ ৪৮৭১=৩৬০০+১২৬০+১১ = ১X৩৬০০+২১X৬০+১১ ।
কিন্তু, ৩৬১১ সংখ্যাটো তেওঁলোকে প্ৰকাশ কৰিব কেনেকৈ? চিত্ৰ–৭ ত দেখুওৱাৰ দৰে? কাৰণ, ৩৬১১=১X৩৬০০+১১ । কিন্তু সেই চিত্ৰটো দেখি কোনোবাই ১X৬০+১১=৭১ বুলি নাভাবিব নে? আনহাতে চিত্ৰ–৮ ত দেখুওৱাটোৰে কি বুজা যাব? ১? নে ৬০? এই সমস্যাটো দূৰ কৰিবলৈ তেওঁলোকে খ্ৰী.পূ. ৭০০–৩০০ মানৰ পৰা সেই খালী স্থানটো বুজাবৰ বাবে এটা চিহ্ন ব্যৱহাৰ কৰিবলৈ ল’লে। চিত্ৰ–১০ ত ফুটটোৰ স্থানত সেই চিহ্নটো ৰাখিলে তাৰ পৰা এতিয়া সুন্দৰকৈ বুজা যাব যে সেইটো ৩৬১১ আৰু চিত্ৰ–৯ ৰ সংখ্যাটো ৬২ । (চিত্ৰসমূহ অঁকাৰ সুবিধাৰ বাবে উদাহৰণসমূহ এই লেখাটোৰ পৰা সংগ্ৰহ কৰা হৈছে: http://www.basic-mathematics.com/babylonian-numeration-syst…)

এই যে খালী স্থানটো উপস্থাপনৰ বাবে এটা চিহ্ন ব্যৱহাৰ কৰা হ’ল, ইয়েই শূন্যৰ ধাৰণাৰ প্ৰাৰম্ভিক খোজ। সেইবাবেই শূন্যৰ অৱিষ্কাৰ বেবিলেনীয়সকলেহে কৰা বুলি কোনো কোনোৱে ক’ব বিচাৰে। ৬০০ খ্ৰী. মানৰ পৰা সেই একেটা উদ্দেশ্যতে ভাৰতীয় গণিতজ্ঞই বৰ্তমান ব্যৱহাৰ কৰা শূন্য আকৃতিৰ চিহ্নটো ব্যৱহাৰ কৰিছিল। এটা চিহ্নক এনেকৈ স্থান নিৰূপক হিচাপে ব্যৱহাৰ কৰা এই ধাৰণাটো বেবিলেনীয়সকলৰ পৰাই ভাৰতীয়সকলে লৈছিল বুলিও কোনো লেখাত পোৱা যায়। এই শূন্য–আকৃতিৰ চিহ্নটো আৰৱীয়সকলে আকৌ তেওঁলোকৰ পাঁচ সংখ্যাটো বুজাবলৈ ব্যৱহাৰ কৰিছিল। এনে কথাবোৰত সম্পূৰ্ণ সত্যতা নিৰূপন কৰাটো বা আমি আহৰণ কৰাটো নিশ্চয় সম্ভৱপৰ নহয়, আৰু সেইটো এই লেখাৰ উদ্দেশ্যও নহয়। ইয়াৰ মূল কথাটো হ’ল— খালী স্থানটো এটা চিহ্নৰে প্ৰকাশ কৰিবলৈ মানুহৰ মনলৈ অহা ধাৰণাটো! এই ধাৰণাটোৱেই গঢ়ি তুলিলে সভ্যতাৰ এটি বৃহৎ বাট।

খালী স্থানটো প্ৰকাশ কৰিবলৈ চিহ্ন হিচাপে ব্যৱহাৰ কৰিবলৈ লোৱাৰ পাছত— যোগ, বিয়োগ, পূৰণ, হৰণ আদিত জড়িত কৰিব পৰাকৈ পৰিমাণ হিচাপে, অৰ্থাৎ এটা সংখ্যা হিচাপে এই শূন্যটোক কেতিয়াৰ পৰা ব্যৱহাৰ কৰা হ’ল? এই প্ৰশ্নটোৰ উত্তৰতেই আছে, ওপৰত উল্লেখ কৰা দ্বিমতখিনিৰ পাছতো শূন্যক ভাৰতীয়সকলে আৱিষ্কাৰ কৰা বুলি পৃথিৱীয়ে মানি অহাৰ কাৰণটো। যদিও সেই খালি স্থানটো বুজাবৰ বাবে বেবিলনীয়সকলেও এটা চিহ্ন ব্যৱহাৰ কৰিছিল, ভাৰতীয়সকলেও আন এটা চিহ্ন ব্যৱহাৰ কৰিছিল, কিন্তু সেই স্থানটো বুজোৱা চিহ্নটোক নৱম শতিকা মানৰ পৰা ভাৰতীয়সকলে ‘একো পৰিমাণ নাই’ অৰ্থত ব্যৱহাৰ কৰিবলৈ আৰম্ভ কৰিলে। অৰ্থাৎ, এটা আছে, দুটা আছে, তিনিটা আছে, এটাও নাই…, এনেকুৱা অৰ্থত। এই এটাও নাইকীয়া অৰ্থত নৱম শতিকাৰ পৰা ভাৰতীয় গণিতজ্ঞই আজিৰ শূন্য–আকৃতিটো ব্যৱহাৰ কৰিলে। অৰ্থাৎ ই স্থান নিৰূপক এটা চিহ্নৰ পৰা এটা সংখ্যালৈ পৰিবৰ্তন হ’ল। ই হ’ল গণিত অধ্যয়নৰ ইতিহাসৰ অতিশয় উল্লেখযোগ্য পৰিঘটনাবোৰৰ এটা, যাৰ বাবেই ভাৰতীয়ই যুগ–যুগান্তলৈ গৌৰৱ কৰি থাকিব পাৰিব। গণিতজ্ঞ Mahāvīraয়ে, শূন্যৰে এটা সংখ্যক পূৰণ কৰিলে শূন্য হয়, এটা সংখ্যাৰ পৰা শূন্য বিয়োগ কৰিলে একেটা সংখ্যাই পোৱা যায় ইত্যাদি কথা লিখি উলিয়ালে। তেওঁ অৱশ্যে ভুলকৈ, এটা সংখ্যাক শূন্যৰে হৰণ কৰিলে সংখ্যাটো অপৰিবৰ্তনীয় হৈ থাকে বুলি অনুমান কৰিছিল। পাছলৈ ভাষ্কৰে ইয়াক অসীম বুলি প্ৰকাশ কৰিলে। এনেদৰেই শূন্য, এটা চিহ্ন আৰু এটা সংখ্যা হিচাপে প্ৰতিষ্ঠিত হ’ল। ইয়াক ‘বীজগণিতৰ দুৱাৰ মুকলি কৰা’ বুলিও কোৱা হয়। আন গণিতজ্ঞ–লেখকৰ জৰিয়তে এই ধাৰণা আন মহাদেশবোৰলৈ গতি কৰিলে। বহু শতিকাৰ পাছলৈকেও আনে এই সম্পৰ্কে একো ধাৰণাই কৰিব পৰা নাছিল।

শূন্যৰ অভাৱে সমীকৰণ সমাধান কাৰ্যও জটিল কৰি ৰাখিছিল। আমি এটা উদাহৰণ ল’ব পাৰোঁ—
আপুনি এটা ডাঙৰ খৰাহীত ৰখা তামোলখিনিৰ পৰা এপোন তামোল বিক্ৰী কৰিছে, আৰু বাকী থকা মাথোঁ কেইটামান তামোল সৰু খৰাহী এটাত থৈ ডাঙৰ খৰাহীটো আজৰাই পেলালে। কামটো কৰিয়েই আপুনি হঠাৎ ক’ৰবালৈ যাব লগা হ’ল। কিন্তু কেইটা তামোল বাকী থাকিল, সেইকেইটা বিক্ৰী কৰিলে আপুনি কিমান ধন পাব, সেই কথাটো জানিবলৈ আপুনি উদগ্ৰীৱ হৈ পৰিছে। আনহাতে, খৰাহী দুটা কিনি আনোতে আকৃতি অনুসৰি দাম লৈছিল,